The author has come up with an amazing application for taking decisions. Game theory is the study of mathematical models of strategic interaction among rational decision-makers. It has a vast range of applications, including defence. The current Indo-China relationship can be reviewed through this theory. This article is the first part.
You might have heard/read about ‘game theory’, probably because of the Academy Awards winning movie ‘A Beautiful Mind’. Striking something? The character played by Russel Crowe was of a famous mathematician who made fundamental contributions to game theory, John Forbes Nash Jr. (popular as John Nash or only Nash). Dr Nash is the only person to be awarded both the Nobel Memorial Prize in Economic Sciences and the Abel Prize. The Nobel Prize he received in 1994 was for his 28-page PhD dissertation on non-cooperative games he wrote in 1950 at the Princeton University. Although the history of game theory could be traced back to 18th century, it wasn’t until 1928 when famous mathematician John von Neumann published the paper ‘On The Theory of Games of Strategy’ that it came into existence as a unique field.
Game theory is the study of mathematical models of strategic interaction among rational decision-makers. It has a vast range of applications, including defence (shouldn’t be surprising, the defence would probably be among the top complex strategic interactions). In this article, I would be revisiting a research work by one of the world’s foremost econometricians, Arnold Zellner published in The Journal of Conflict Resolution. Why it’s important for countries to discuss issues? Why do countries talk more and fight rarely? Why two big countries maintain the status quo for a piece of land instead of attacking? Why a rich country doesn’t increase its military in another country and just capture it? Let’s try to understand some of them.
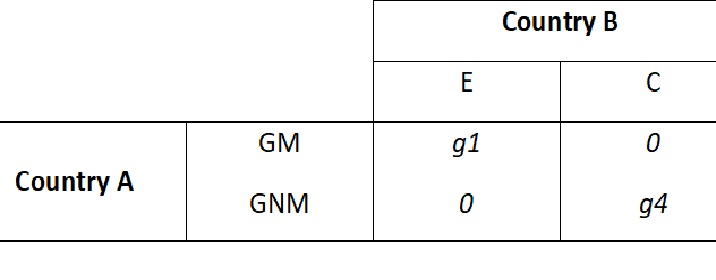
Consider, A and B be two power players in a game of world politics for uncommitted nations (could be also seen as a piece of land or oil reservoir etc.). Also, A has a ‘peace objective’ (rules out military action, remember UN!). Let the pay-off matrix (visual representation of the possible outcomes of the strategic decision) for the game be:
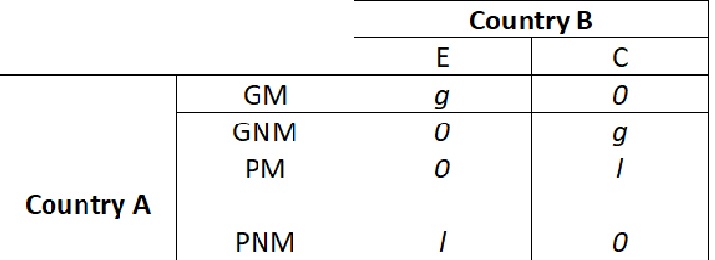
Country A has 4 possible strategies
GM – to have Good Military assistance program.
GNM -to have Good Non-Military assistance program
PM – to have Poor Military assistance program
PNM- to have Poor Non-Military assistance program
Country B has 2 possible strategies
E – to have limited military expansion
C – coexistence
g – gaining, l – losing, 0- no game
How to Resolve?
Just to explain a bit, if Country – A follows good military assistance program and Country – B has a limited military expansion, A would gain nations. What’s making the game a bit complicated? Country A’s peace objective (the condition!)
Who would win this game? Who would gain nations/land/oil reservoir? Well, it might look like Country A but Country B also knows A’s possible strategies, not to be forgotten. If Country A uses GM/GNM it would gain nations from Country B, B is also aware of this. Country B might not even play this ‘unfair’ game in a real setting, rather resort to some strategy not even part of this game and unknown to Country – A (like air or nuclear attack).
As Country – A knows, Country – B might even play the game, seeing the danger it constructs four subgames from the game (remember Country – A has a peace objective).
I.
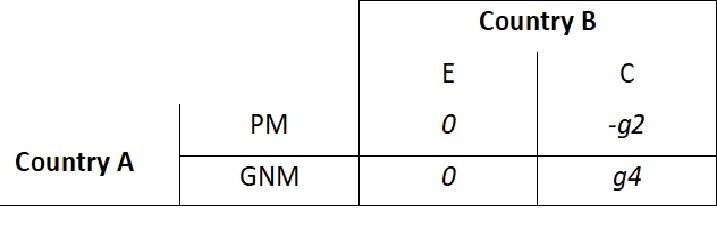
II.
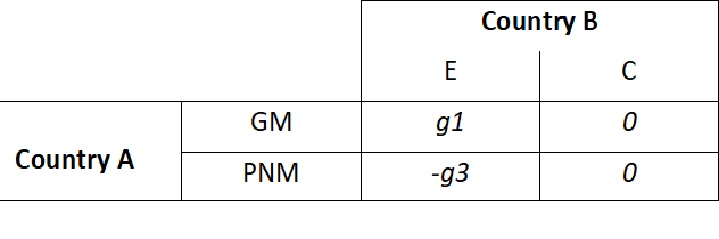
III.

IV.
where all gi’s > 0.
Out of the four games, only two of them are ‘fair’ (having value 0, which B would like to play). Other two, game III and game IV would have negative and positive values of the game respectively (do you think Country A would play game III and B would play game IV? situation is very similar to the main game). Now, for the game I, country B would definitely use strategy E (i.e. with probability 1). Why? Clearly, it knows country A is going to use strategy GNM to gain nations. Also, the question arises would country A play game I? No, as it has a better game which it could play. Game II is also fair and also satisfies A’s peace objective. It’s very clear that in the game IV, B would definitely not use strategy E (i.e. with probability 0). Country A would convince B to play game II, avoiding the danger of B’s not playing at all. Hence, A’s poor non-military assistance program gives B an inducement to coexist.
Now, what if B somehow becomes rich enough to finance its own assistance programs? We would be looking at the same in the follow-up article, Game Theory & Strategy – 2.
Although game theory has progressed a lot in the past decades, classic old examples still maintain their significance and play a great role in the understanding of the subject. In future articles, I would be looking at other such strategies and examples. Hope you enjoyed it!
Title Image Courtesy : https://pt.slideshare.net/aseldis/
References –
- Zellner, A. (1962) ‘War and peace, a fantasy in game theory’, Journal of Conflict Resolution, 6: 39-41.
- https://en.wikipedia.org/wiki/Game_theory
- https://en.wikipedia.org/wiki/John_Forbes_Nash_Jr.
- https://en.wikipedia.org/wiki/John_von_Neumann
- https://senate.universityofcalifornia.edu/_files/inmemoriam/html/arnoldzellner.html
Disclaimer: The views and opinions expressed by the author do not necessarily reflect the views of the Government of India and Defence Research and Studies